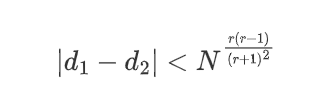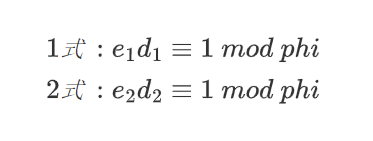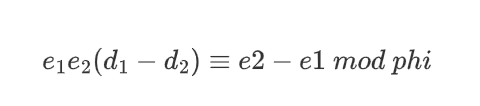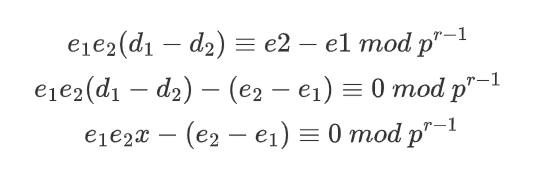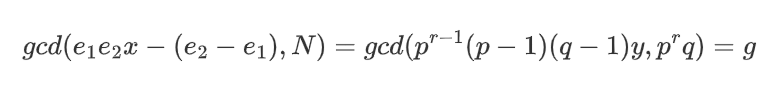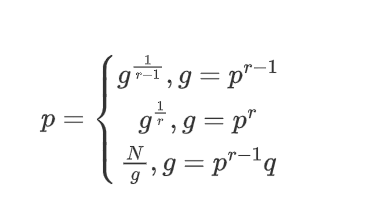D3CTF--d3factor复现

复现了一下d3ctf里遇到的题

题目与解法

上题目代码

from Crypto.Util.number import bytes_to_long, getPrime
from secret import msg
from sympy import nextprime
from gmpy2 import invert
from hashlib import md5

flag = 'd3ctf{'+md5(msg).hexdigest()+'}'
p = getPrime(256)
q = getPrime(256)
assert p > q
n = p * q
e = 0x10001
m = bytes_to_long(msg)
c = pow(m, e, n)

N = pow(p, 7) * q
phi = pow(p, 6) * (p - 1) * (q - 1)
d1 = getPrime(2000)
d2 = nextprime(d1 + getPrime(1000))
e1 = invert(d1, phi)
e2 = invert(d2, phi)

print(f'c = {c}')
print(f'N = {N}')
print(f'e1 = {e1}')
print(f'e2 = {e2}')
'''
c = 2420624631315473673388732074340410215657378096737020976722603529598864338532404224879219059105950005655100728361198499550862405660043591919681568611707967
N = 1476751427633071977599571983301151063258376731102955975364111147037204614220376883752032253407881568290520059515340434632858734689439268479399482315506043425541162646523388437842149125178447800616137044219916586942207838674001004007237861470176454543718752182312318068466051713087927370670177514666860822341380494154077020472814706123209865769048722380888175401791873273850281384147394075054950169002165357490796510950852631287689747360436384163758289159710264469722036320819123313773301072777844457895388797742631541101152819089150281489897683508400098693808473542212963868834485233858128220055727804326451310080791
e1 = 425735006018518321920113858371691046233291394270779139216531379266829453665704656868245884309574741300746121946724344532456337490492263690989727904837374279175606623404025598533405400677329916633307585813849635071097268989906426771864410852556381279117588496262787146588414873723983855041415476840445850171457530977221981125006107741100779529209163446405585696682186452013669643507275620439492021019544922913941472624874102604249376990616323884331293660116156782891935217575308895791623826306100692059131945495084654854521834016181452508329430102813663713333608459898915361745215871305547069325129687311358338082029
e2 = 1004512650658647383814190582513307789549094672255033373245432814519573537648997991452158231923692387604945039180687417026069655569594454408690445879849410118502279459189421806132654131287284719070037134752526923855821229397612868419416851456578505341237256609343187666849045678291935806441844686439591365338539029504178066823886051731466788474438373839803448380498800384597878814991008672054436093542513518012957106825842251155935855375353004898840663429274565622024673235081082222394015174831078190299524112112571718817712276118850981261489528540025810396786605197437842655180663611669918785635193552649262904644919
'''

分析

flag = 'd3ctf{'+md5(msg).hexdigest()+'}'
p = getPrime(256)
q = getPrime(256)
assert p > q
n = p * q
e = 0x10001
m = bytes_to_long(msg)
c = pow(m, e, n)

普通的RSA加密，但n，p，q未知

N = pow(p, 7) * q
phi = pow(p, 6) * (p - 1) * (q - 1)
d1 = getPrime(2000)
d2 = nextprime(d1 + getPrime(1000))
e1 = invert(d1, phi)
e2 = invert(d2, phi)

这一段是将原来的n与phi都乘上了p⁶,然后生成了2000bits的质数d1与d2.从d2的生成代码可知，d1与d2的高位是相同的。之后通过求逆元的方式得到了e1，e2

解题

没见过的RSA变式加密很有可能在论文中找到。这道题就是如此，论文为：399.pdf (iacr.org)

在论文中可以找到一模一样的加密方式与攻击手段，但还是要验证攻击方式是否可用

题中给出的r=6，d1，d2为2000bits，N为2048bits。很容易得知

img

因此满足论文中所给出的攻击方法

接下来按照论文进行运算

img

用1式乘上e2减去2式乘上e1，得到

img

根据同余式的性质，因为phi=p^r-1(p-1)(q-1),所以上式等于

img

因此，在满足|d1-d2|<Nⁱ（这里i=r(r-1)/(r+1)²）的情况下，有如下式子

img

解出g有以下情况

img

照此思路就能得到p、q，从而得到flag。但难点在于x的计算存在困难。论文的示例中提到可以采用LLL算法来计算多项式方程的解，也可以用coppersmith攻击来求多项式的小根。使用sagemath可以很容易实现

解题代码

from Crypto.Util.number import *
from hashlib import *
import gmpy2
c=2420624631315473673388732074340410215657378096737020976722603529598864338532404224879219059105950005655100728361198499550862405660043591919681568611707967
N=1476751427633071977599571983301151063258376731102955975364111147037204614220376883752032253407881568290520059515340434632858734689439268479399482315506043425541162646523388437842149125178447800616137044219916586942207838674001004007237861470176454543718752182312318068466051713087927370670177514666860822341380494154077020472814706123209865769048722380888175401791873273850281384147394075054950169002165357490796510950852631287689747360436384163758289159710264469722036320819123313773301072777844457895388797742631541101152819089150281489897683508400098693808473542212963868834485233858128220055727804326451310080791
e1=425735006018518321920113858371691046233291394270779139216531379266829453665704656868245884309574741300746121946724344532456337490492263690989727904837374279175606623404025598533405400677329916633307585813849635071097268989906426771864410852556381279117588496262787146588414873723983855041415476840445850171457530977221981125006107741100779529209163446405585696682186452013669643507275620439492021019544922913941472624874102604249376990616323884331293660116156782891935217575308895791623826306100692059131945495084654854521834016181452508329430102813663713333608459898915361745215871305547069325129687311358338082029
e2=1004512650658647383814190582513307789549094672255033373245432814519573537648997991452158231923692387604945039180687417026069655569594454408690445879849410118502279459189421806132654131287284719070037134752526923855821229397612868419416851456578505341237256609343187666849045678291935806441844686439591365338539029504178066823886051731466788474438373839803448380498800384597878814991008672054436093542513518012957106825842251155935855375353004898840663429274565622024673235081082222394015174831078190299524112112571718817712276118850981261489528540025810396786605197437842655180663611669918785635193552649262904644919
e=0x10001
PR.<x> = PolynomialRing(Zmod(N))
f=e1*e2*x-(e1-e2)
f=f.monic()
k=f.small_roots(beta = 0.5, epsilon = 0.4, X = 2^1000)[0]
#k=6026188071205144053368734157378113871998610498635758102306924949208539409278951959968138902906878320358536089190856063838203652085411343275918136041503018654914512075174785716697544493562866611023489700861401711316474669786472712436070391719434465362891545258455898553431580803183299730942414936305178
p7=gmpy2.gcd(e1*e2*k-(e1-e2),N)
p=gmpy2.iroot(p7,6)
#p=81911394167511996830305370213894554209992159667974516868378702592733037962549
q=N//p**7
#q=#59689394622751323780317475130818337618980301243859922297121750335804594909859
n=p*q
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=long_to_bytes(gmpy2.powmod(c,d,n))
flag = 'd3ctf{'+md5(m).hexdigest()+'}'
print(flag)

flag:d3ctf{42f79e777e622aef5344b04ad6233130}

总结

这是第一道复现的大赛题目，难度肯定是有的，复现的过程中也遇到了很多疑惑的地方，但最终还是复现出来了

参加d3也收获了许多经验，比如可以搜论文来解题，不要总想着硬啃

之后要干的事就是多看点书，多做点题，把数学知识补一补，学习一下LLL算法，small_root,coppersmith和sagemath