关于LFSR的原理以及攻击方式

学习了一下LFSR

一个LFSR由若干时钟存储元件（触发器）和一个反馈路径组成。存储元件的数目即为LFSR的度，即一个拥有m个存储元件的LFSR可称为“度为m”。反馈网络计算位移寄存器中某些触发器的XOR和，并将其作为上一个触发器的输入。

举个简单的LFSR例子：

img

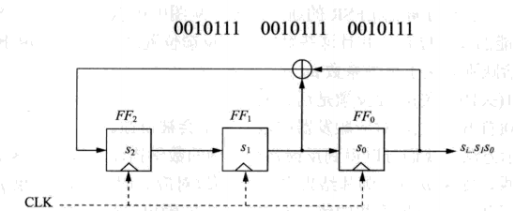
图为拥有三个触发器FF₀,FF_{1,FF2的LFSR，即此LFSR的度为3，反馈路径如图所示，内部状态用si表示。在每个时钟滴答内，内部状态会向右移动一位。最右边为LFSR的输出位，最左边位输入位。输入位的状态是在反馈路径中计算的，它是前面时钟周期中一些触发器的XOR和。}

假设初始状态s₀=0、s₁=0、s₂=1，则计算可得此LFSR产生的序列为0100111，周期长度为7

据此可写出计算LFSR输出位的公式：

假设初始状态位s₀、s₁、s₂，可得

其中i=0,1,2...

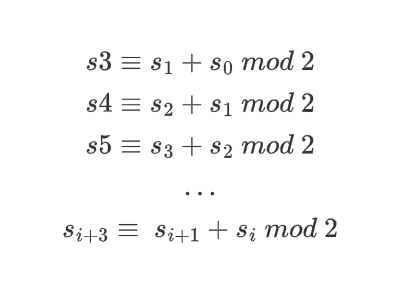
这个例子非常简单，但阐明了LFSR的原理，接下来看看通用的LFSR

1.LFSR的数学描述

img

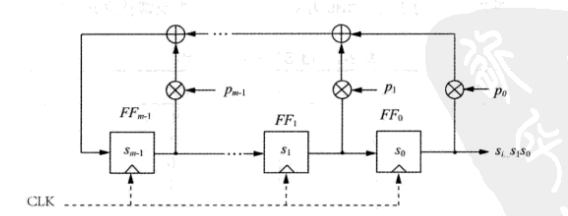
这张展示了一个度为m的LFSR，这个LFSR拥有m个可能的反馈位置，触发器与反馈位置通过XOR连接。之所以将反馈位置称为“可能”，是因为每条反馈路径的活跃与否取决于p₀,p₁,p₂,...,p_m-1：

• 如果p_i=1(关闭开关)，此反馈是活跃的
• 如果P_i=0(打开开关)，对应触发器的输出将不会反馈

于是可以将一个触发器的输出通过输出值与对应系数的乘积来表示，即p_i*s_i

假设某个LFSR的初始加载值为s₀,s₁,s₂,...,s_m-1,则下一个输出位可通过触发器输出值与对应系数的乘积的XOR和表示：

下一个为

归纳一下，输出序列可描述为：

此处提出一定理：度为m的LFSR可以产生的最大序列长度为2^m-1

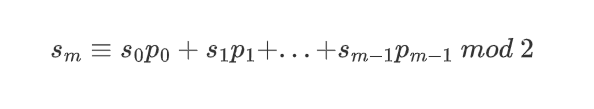
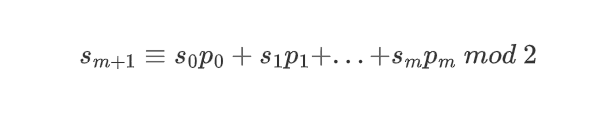
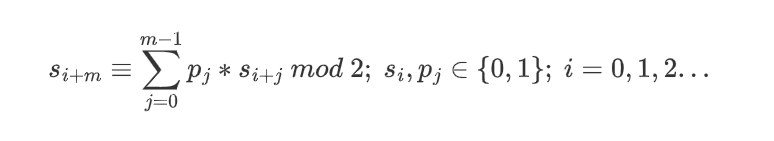
2.关于LFSR的其它属性

LFSR通常用以下多项式来指定：反馈系数向量为(p_m-1,p_m-2,p_m-3,...,p₀)的LFSR可以表示为以下多项式：

例如，系数为(p₃=0,p₂=0,p₁=1,p₀=0)d的LFSR可以表示为多项式：x⁴+x+1

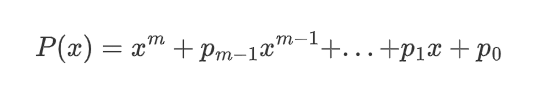
当LFSR拥有最大长度（即周期）时，对应的的反馈系数向量多项式被称为本原多项式。对于一个给定的度m而言，可能存在多个本原多项式

3.针对单个LFSR的攻击

谈完了LFSR的原理，现在来说一下针对LFSR的攻击方式

假设攻击者Oscar知道部分明文和对应的密文，他就可以发起攻击。假设Oscar知道明文x₀,x₁,...,x_2m-1，它们对应的密文为y₀,y₁,...y_2m-1。Oscar利用这2m对明文和密文位，就可以重构开头的2m个密钥序列

接下来就是计算出反馈系数向量p_i。根据输出序列的公式，可以得到如下式子

上述等式中每一个都是线性无关的，故现在有了含m个未知数P_m-1,...,p₁,p₀的m个线性等式。利用高斯消去或矩阵求逆等求解方程便可以构造出反馈系数向量，并以此计算任意m个输出位，得到整个输出序列。正因为这种强大的攻击方式，不少序列密码都是使用多个LFSR组合的方式构建强壮的密码体制，Trivium就是一个很好的例子

img

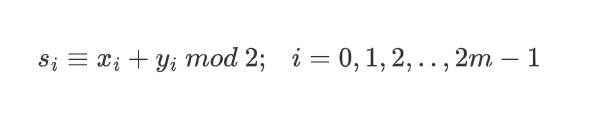
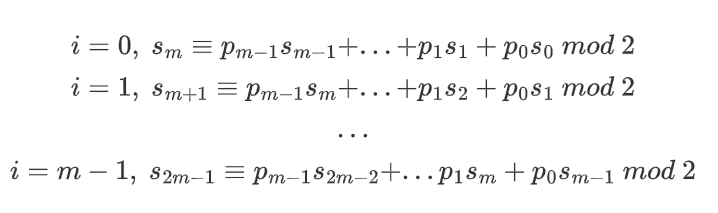
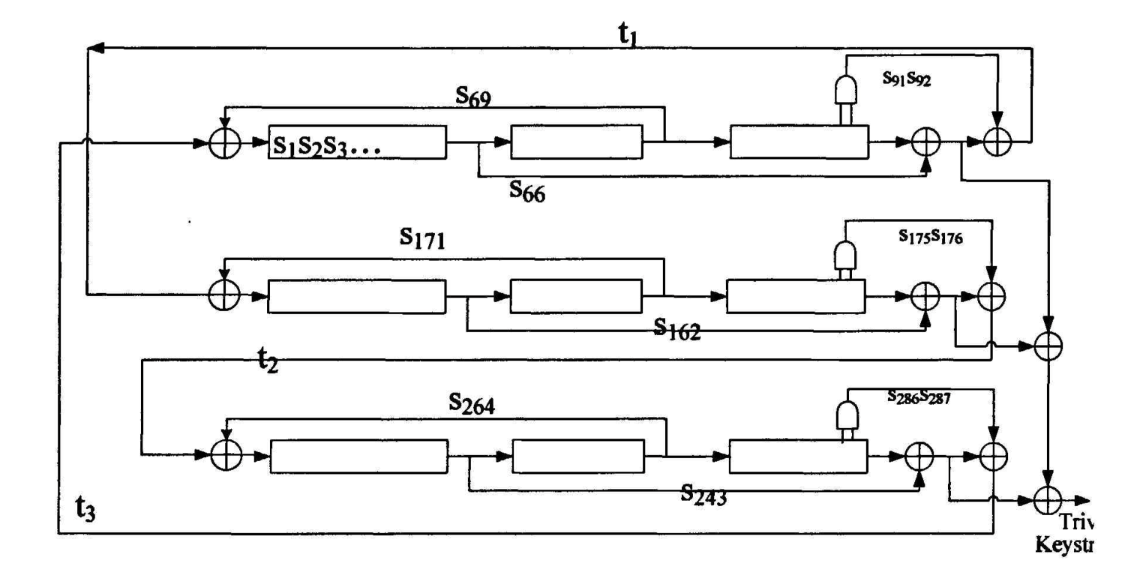
注：插图来自《深入浅出密码学》